
Why Addition Is Actually Easy — If You Break It Down Right
What's the problem?
To many adults, a problem like 368 + 477 is second nature. You stack the numbers, carry the digits, and move on. But if you watch a young child wrestle with it, you’ll quickly realize: there’s nothing obvious about the process.
The mysterious little “1” above the columns? The switch from ones to tens? It’s confusing — and unnecessarily so.
Why it's harder than it looks
Adding numbers like 368 + 477 may look simple, but it contains layers of logic:
- Kids need to understand place value — that the “6” and “7” mean 60 and 70
- They have to add each column sequentially
- The need to understand how to carry digits
That’s three distinct pieces of thinking which need to be held in working memory at once. For a developing learner, that’s asking a lot. And if just one part isn’t solid, the whole process breaks down.
Step One: Simplify the structure
Before even doing any math, you can make the problem easier — just by laying it out the right way.
Imagine a worksheet where every digit has a box: one above for carrying, one below for answers.
This layout sends powerful early signals — like:
- "I see two carry digits."
- "There are three answer digits."
The structure immediately reduces cognitive demands of the problem.
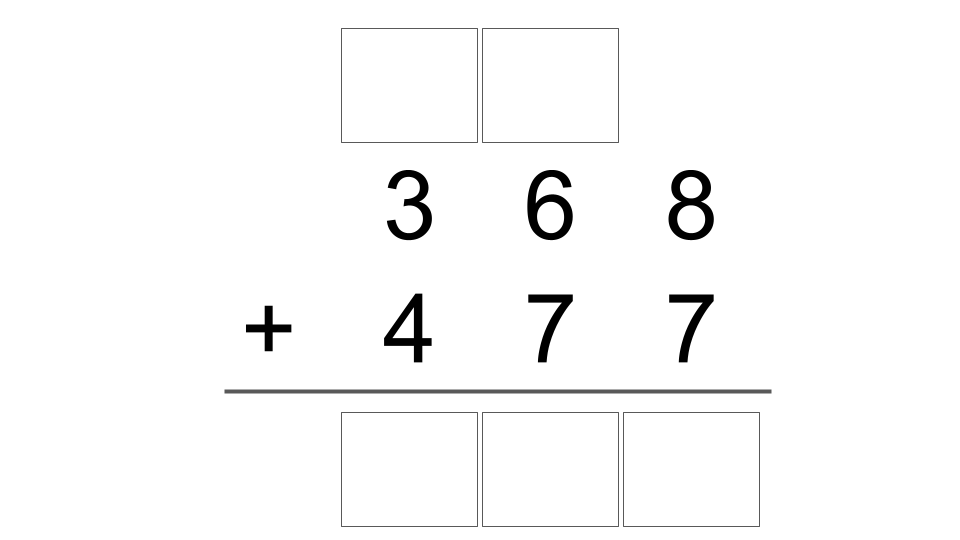
Step Two: Reduce the size of the task
Now, layer on the second simplification: don’t show the whole problem at once.
Just show the first step.
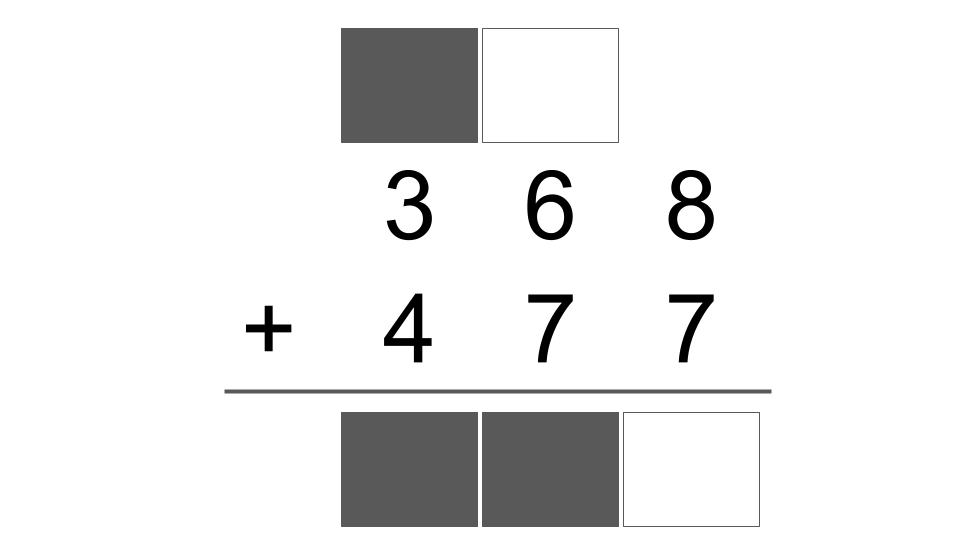
Let the student solve 8 + 7 = 15. Then they carry the 1, write the 5 — then move to the next column.
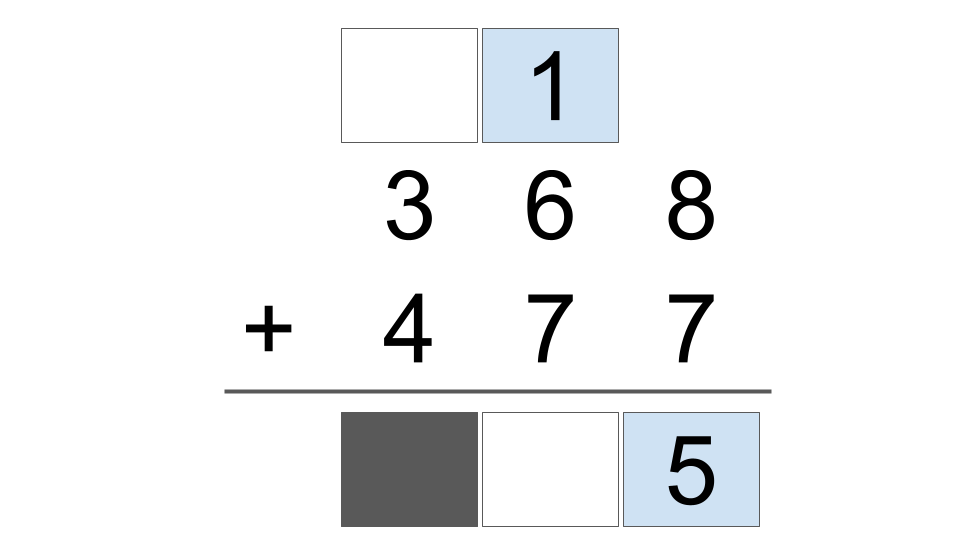
Do the same for the next step 1 + 6 + 7 = 14. They carry the 1, write 4 — then move to the next column.
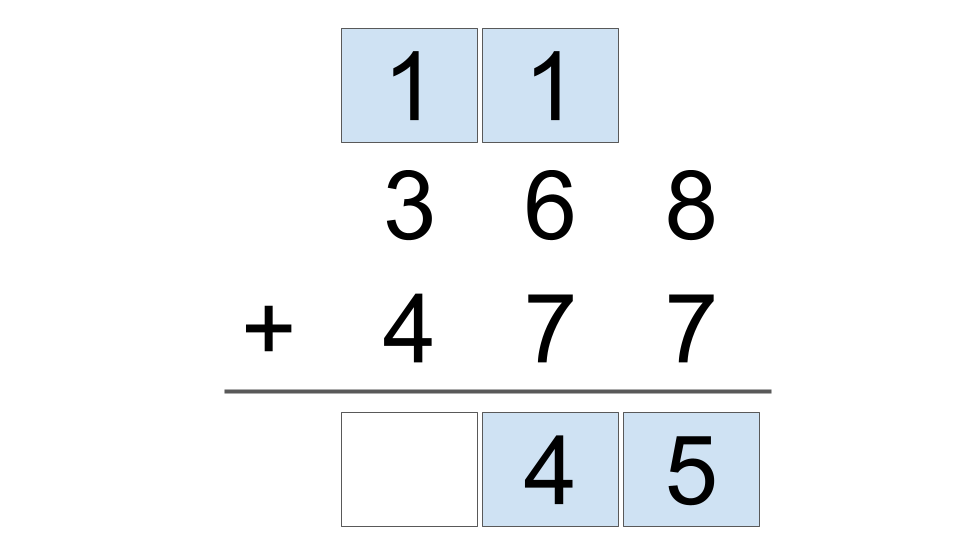
Finally, solve the last column 1 + 3 + 4 = 8. Write 8.
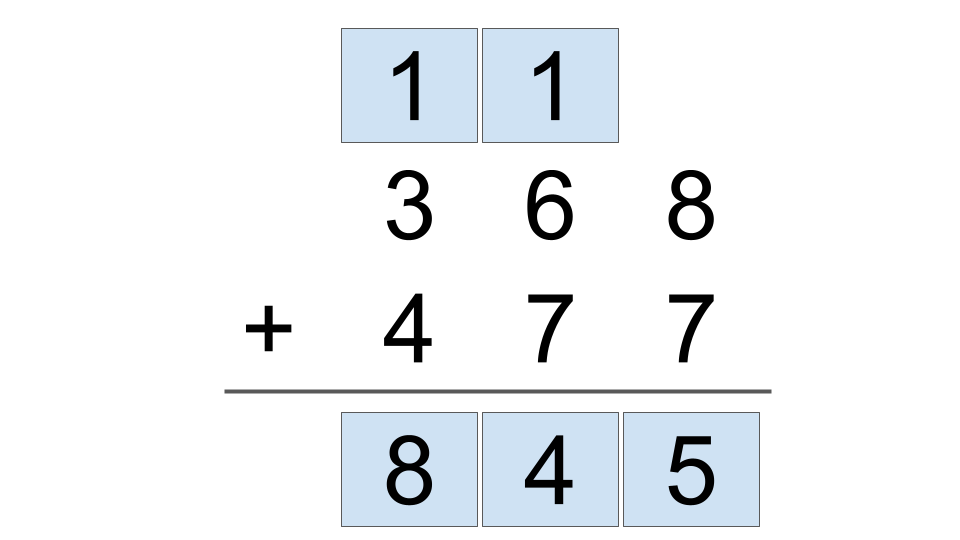
The addition problem has been simplified.
The bottom line
Addition isn't naturally hard. We just make it feel hard by giving kids too much at once.
When we:
- Structure problems clearly
- Sequence them step by step
— confusion disappears. Confidence takes its place.
At MathStairs, we believe real progress comes from building skills carefully — laying strong foundations so students can move faster and think bigger as they grow.
Stay tuned. We’re building something to make smart, confident math thinking the norm — not the exception.